ThinkDifferent

Look at this 2D layout of a construction having eight compartments, with green blocks representing the doors connecting the respective compartments.

(Well, I agree that's a poor design! A person in the lawn can enter in only through the JunkYard(JY) or through the RestRoom(RR)! Now it's too late; the construction ready to be released. We gotta live with it! But I strongly recommend the designer of the layout to study Design-Patterns. Visit http://patternosophy.blogspot.com/ and participate in design-discussions)

You're the unfortunate person asked for surveying the compartments. You must pass through each door exactly once (assume, the door locks when you pass though it!) and you must visit each and every compartment (well, more than once, if you wish to).

You can choose to start from any compartment. Don't worry about 'how will you reach there' in the first place (assume, you will be teleported there. After that, you'll use the green doors to move around!). Remember, you are done, when all the compartments are visited at least once and all the doors are locked (You'll be teleported back, out of the house!).

Draw out a plan of your visit. Bonus, if you could count all such plans possible!

(a) The quadratic x² + ax + b + 1 has roots which are positive integers. Show that (a² + b²) is composite (i.e. has factors).

Hint: What? You wants hints? Not for this one!

(b) Additionally, prove that, if a² = 4(b + 1), (a² + b²) becomes a perfect square.

(a) Let there be a binary(0, 1) matrix T[8*8] =

0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 1

Let me define:

1. a boolean product (x.y), for any two binary numbers x and y, as:
x.y = 1, if and only if x = y = 1

2. a boolean sum (x + y), for any two binary numbers x and y, as:
x + y = 0, if and only if x = y = 0

3. a Boolean-Matrix-Multiplication as the normal matrix multiplication, that uses boolean product and sum, instead of the usual (base-10) arithmetic product and sum respectively.

Find the minimum number m such that

T.T.T...(m times) = T.T.T...(m+k times)

for any integer k > 1, where T.T represents Boolean-Matrix-Multiplication of T with T.

(b) How (if at all) will the answer change, if T were a symmetric boolean matrix as:

0 1 0 0 0 0 0 0
1 0 1 0 0 0 0 0
0 1 0 1 0 0 0 0
0 0 1 0 1 0 0 0
0 0 0 1 0 1 0 0
0 0 0 0 1 0 1 0
0 0 0 0 0 1 0 1
0 0 0 0 0 0 1 1

Hint: find

T.T.T...(m times) = T.T.T...(m+2k times)

for any integer k > 1.

OK! Now some algebra.

The real set {a, b, c} is such that the equation

x³ + ax² + bx + c = 0

has three distinct real roots and

(x² + x + 2005)³ + a(x² + x + 2005)² + b(x² + x + 2005) + c > 0

for all real values of x. Show that, for the same set {a, b, c},

(2005)³ + a(2005)² + b(2005) + c > 1/64

Two beggars A and B managed to get a 13-litres-jar full of Vodaka . They have two more jars of 5 and 10 litres respectively. They decided to divide the amount equally, with the aid of the jars and leave the undivided amount for a third beggar C, who was near by. What's the maximum amount the beggars A and B can have, if they are to use only the jars available with them to make the division? Also show the steps to make the division.

Hint: Is it possible to make a division (6 + 6 + 1)?

There are two identical jars W and V, containing equal amounts of Water and Vodka respectively. I take a spoon and transfer a spoonful of Vodka from V to W and dissolve it completely. Now I use the same spoon to transfer a spoonful of the liquid (mixture) from W to V and dissolve it completely.

Now both the jars contain the same amount of liquid, but in diferent ratios of the original components. Which jar has the greater quantity of the other component? That's, whether the Vodka in jar W is more that the Water in the jar V, or the other way?

In a Merry-Go-round, with all seats occupied, the 5th guy is exactly facing the 19th guy. How many seats are there in the Merry-Go-round?

A train leaves station A at x hours y minutes and arrives station B at y hours z minutes. The duration of the journey is z hours x mins. Find all possible value of x, the hour (there could be more than one answers) the train leaves the station A. Assume the clock moves from 00:00 to 24:00.

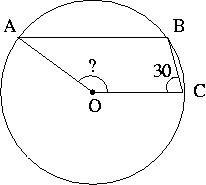
In the above diagram, a line CB is projected from C at an angle 30-degrees from OC., intersecting the circle at B. From B a chord BA parallel to OC is drawn. Find the angle AOC.

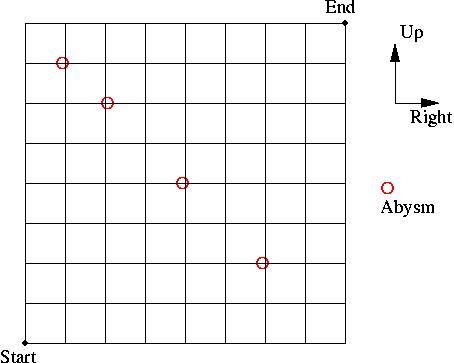
fig1

A drunkard starts from the Start and wants to reach the End. He can move only in the Up and Right directions, along the edges of the small squares, as shown. He can't turn back. On his way there could be abysms, indicated by the circles. He can't reach End if he falls into one of those abysms. What is the probability that the drunkard will reach the End?

fig2

In the above triangle ABC, AB = 3 units and AC = 4 units. The median AD to BC is half of BC in length, as indicated in the figure. Find the area of the triangle ABC.

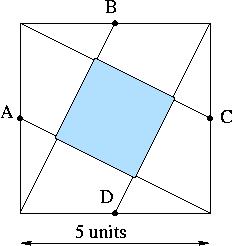
fig1

In the above square of size 5 units, {A, B, C, D} are four mid points of the corresponding sides. Find the area of the shaded region.

Well, we know the importance of exercising. Centuries ago, an average human life involved sufficient activities to give the body necessary exercise. Our lives have changed so much! Now we need to exercise. So, we created Gyms so that, our body gets the daily exercise needed.

Here we have the Gym for the brain! I din't say, we don't get sufficient problems to get our brain working on. We have enough problems, related to our profession, to solve. But those restrict the class of people who can enjoy solving them.

The problems we discuss here are of more basic in nature. We all have studied those concepts sometimes in past, in our school lives. Let's revisit them, see if we really can solve some of them!

Let's give our brain some aerobics!

-- Daily aerobics is better than once-a-week powerlift!