Monday, June 20, 2005
Problem# 3
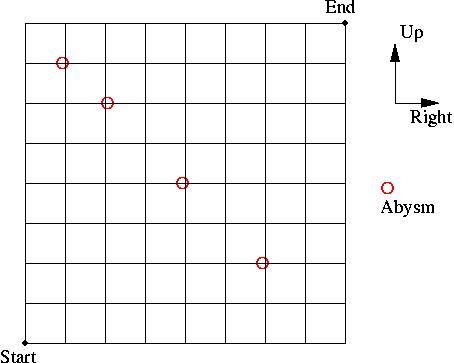
fig1
A drunkard starts from the Start and wants to reach the End. He can move only in the Up and Right directions, along the edges of the small squares, as shown. He can't turn back. On his way there could be abysms, indicated by the circles. He can't reach End if he falls into one of those abysms. What is the probability that the drunkard will reach the End?
Comments:
<< Home
total no of ways= 16!/(8!)^2 = 12870.
no of ways in which the path goes through the abysm are:
= (8!/(7!*1!))^2 + (8!/(6!*2!))^2 + (8!/(4!)^2)^2 + (8!/(2!*6!))^2
= 64 + 784 + 4900 + 784
= 6532.
thus the required probablity is:
= 6532/12870
= 0.5075
no of ways in which the path goes through the abysm are:
= (8!/(7!*1!))^2 + (8!/(6!*2!))^2 + (8!/(4!)^2)^2 + (8!/(2!*6!))^2
= 64 + 784 + 4900 + 784
= 6532.
thus the required probablity is:
= 6532/12870
= 0.5075
That's wrong!
I guess, you forgot that, once the man goes into the gutter, he can never reach the END. There is no question of "through the abysm"! [:)]
I guess, you forgot that, once the man goes into the gutter, he can never reach the END. There is no question of "through the abysm"! [:)]
Total Number of ways to reach the End = 16!/(8! * 8!) = 12870
From this we need to remove all those paths that pass through the 4 abysms.
1.First Abysm [1 RIGHT, 7 UP]
Total number of paths passing through this one = 8C1 * 8C1 =64
2.Second Abysm [2 RIGHT, 6 UP]
Total number of paths passing through this one = 8C2 * 8C2 =784
3.Thrid Abysm [4 RIGHT, 4 UP]
Total number of paths passing through this one = 8C4 * 8C4 =4900
4.Fourth Abysm [6 RIGHT, 2 UP]
Total number of paths passing through this one = 8C2 * 8C2 =794
So total number of paths to be removed = 64+784+4900+784 = 6532
Required Prob =(12870-6532)/12870
= 0.49246309246309246309246309246309
From this we need to remove all those paths that pass through the 4 abysms.
1.First Abysm [1 RIGHT, 7 UP]
Total number of paths passing through this one = 8C1 * 8C1 =64
2.Second Abysm [2 RIGHT, 6 UP]
Total number of paths passing through this one = 8C2 * 8C2 =784
3.Thrid Abysm [4 RIGHT, 4 UP]
Total number of paths passing through this one = 8C4 * 8C4 =4900
4.Fourth Abysm [6 RIGHT, 2 UP]
Total number of paths passing through this one = 8C2 * 8C2 =794
So total number of paths to be removed = 64+784+4900+784 = 6532
Required Prob =(12870-6532)/12870
= 0.49246309246309246309246309246309
When 4 absyms are put in grid of 8*8 in the diagonal, the probability of reaching the End becomes 0.5.
I do not understand, "Why do you consider 16 steps?"
The fact is, after 8 steps only, you know whether he will reach the End or not! As simple as that.
I guess now you know what the correct answer is!
-Sujeet
Post a Comment
The fact is, after 8 steps only, you know whether he will reach the End or not! As simple as that.
I guess now you know what the correct answer is!
-Sujeet
<< Home


