Sunday, June 26, 2005
Problem# 4
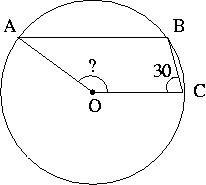
In the above diagram, a line CB is projected from C at an angle 30-degrees from OC., intersecting the circle at B. From B a chord BA parallel to OC is drawn. Find the angle AOC.
Comments:
<< Home
the diagram is incorrect because if OCB is 30 AOB will be 60 and not obtuse as shown in diagram.
Let angle BCO= C
constrction: extend CO to touch the circle at point D.
angle ABC = 180 - C (since AB || CD)
angle DBC = 90(Angle in semi circle)
angle ABD = 180 - C-90 = 90 -C
angle AOD = 2*(angle ABD)(angle at centre is twice )
= 2 *(90 -C)= 180 -2C
angle AOC = 180 - (180 - 2C)= 2C
Let angle BCO= C
constrction: extend CO to touch the circle at point D.
angle ABC = 180 - C (since AB || CD)
angle DBC = 90(Angle in semi circle)
angle ABD = 180 - C-90 = 90 -C
angle AOD = 2*(angle ABD)(angle at centre is twice )
= 2 *(90 -C)= 180 -2C
angle AOC = 180 - (180 - 2C)= 2C
I repeat-- "Assume 'theta' if you have any problems with 30-degrees!
"
The geometric-realization stays valid for a general theta.
Also, if two parallel lines are intersected by a transversal, then the internal angles are either 'equal' or 'supplementary'
-- says a maths book of 5th stsndard!
Hope you enjoyed solving this!
-Sujeet
"
The geometric-realization stays valid for a general theta.
Also, if two parallel lines are intersected by a transversal, then the internal angles are either 'equal' or 'supplementary'
-- says a maths book of 5th stsndard!
Hope you enjoyed solving this!
-Sujeet
HI!
I just want you to understand why i don't like 30 degrees. (I'm the one who posted the first comment.) If that angle is not bigger than 45 degrees, you can't draw a quadrangle like the one on your picture. I mean AB and OC can't be aralell.
In this case the theorem you mentioned can't be used.
I just want you to understand why i don't like 30 degrees. (I'm the one who posted the first comment.) If that angle is not bigger than 45 degrees, you can't draw a quadrangle like the one on your picture. I mean AB and OC can't be aralell.
In this case the theorem you mentioned can't be used.
Hmmm, well, I didnt measure the angle accurately. But, I did mention how the construction proceeds. Don't go by my diagram, you are free to make one yourself!
But the idea is, the value of 'theta' does not matter. Take any value of theta (say, 1, 5, 30, 45, 30, 60, 120). The answer is always twice theta.
Hope this clarifies my intent to post this problem.
But the idea is, the value of 'theta' does not matter. Take any value of theta (say, 1, 5, 30, 45, 30, 60, 120). The answer is always twice theta.
Hope this clarifies my intent to post this problem.
Abe yaar, the angle OCB cant be less than 45 bcoz at 45 the line BA is a tangent to the circle. And for OCB less than 45 AB will not exist unless u draw the line in the opposite direction. then thediagram would be like an x with two horizontal lines joining the corners.
Post a Comment
<< Home


