ThinkDifferent

This one is for the programmers!

You are given an array of integers of size=1001. Each element has exactly one duplicate (that's, every number occurs exactly twice), except one. Find the odd number out, making only one pass through all the 1001 elements of the array and without corrupting the contents of the array. You can use atmost two variables to store temporary evaluations.

This one is adapted from one in the "Puzzles" community of the Orkut (http://www.orkut.com).

You are given a balance that can be used to compare the weight of two objects.

(a) You have a pack of 8 identical balls, 7 of gold and one of iron. It's impossible to identify the iron ball just looking at the balls. You are asked to find out the odd ball using the balance. In how many (minimum) turns can you do it? You may use the fact the iron ball is heavier than the gold ball.

(b) You are given a different pack of 8 balls, 7 of gold and one of unknown material. Using three weighings only, how can you find out the odd ball? Given that, all the balls are visually identical.

Problems yet to be solved correctly, so far:
3 5 9 10 11

Look at this 2D layout of a construction having eight compartments, with green blocks representing the doors connecting the respective compartments.

(Well, I agree that's a poor design! A person in the lawn can enter in only through the JunkYard(JY) or through the RestRoom(RR)! Now it's too late; the construction ready to be released. We gotta live with it! But I strongly recommend the designer of the layout to study Design-Patterns. Visit http://patternosophy.blogspot.com/ and participate in design-discussions)

You're the unfortunate person asked for surveying the compartments. You must pass through each door exactly once (assume, the door locks when you pass though it!) and you must visit each and every compartment (well, more than once, if you wish to).

You can choose to start from any compartment. Don't worry about 'how will you reach there' in the first place (assume, you will be teleported there. After that, you'll use the green doors to move around!). Remember, you are done, when all the compartments are visited at least once and all the doors are locked (You'll be teleported back, out of the house!).

Draw out a plan of your visit. Bonus, if you could count all such plans possible!

(a) The quadratic x² + ax + b + 1 has roots which are positive integers. Show that (a² + b²) is composite (i.e. has factors).

Hint: What? You wants hints? Not for this one!

(b) Additionally, prove that, if a² = 4(b + 1), (a² + b²) becomes a perfect square.

(a) Let there be a binary(0, 1) matrix T[8*8] =

0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 1

Let me define:

1. a boolean product (x.y), for any two binary numbers x and y, as:
x.y = 1, if and only if x = y = 1

2. a boolean sum (x + y), for any two binary numbers x and y, as:
x + y = 0, if and only if x = y = 0

3. a Boolean-Matrix-Multiplication as the normal matrix multiplication, that uses boolean product and sum, instead of the usual (base-10) arithmetic product and sum respectively.

Find the minimum number m such that

T.T.T...(m times) = T.T.T...(m+k times)

for any integer k > 1, where T.T represents Boolean-Matrix-Multiplication of T with T.

(b) How (if at all) will the answer change, if T were a symmetric boolean matrix as:

0 1 0 0 0 0 0 0
1 0 1 0 0 0 0 0
0 1 0 1 0 0 0 0
0 0 1 0 1 0 0 0
0 0 0 1 0 1 0 0
0 0 0 0 1 0 1 0
0 0 0 0 0 1 0 1
0 0 0 0 0 0 1 1

Hint: find

T.T.T...(m times) = T.T.T...(m+2k times)

for any integer k > 1.

OK! Now some algebra.

The real set {a, b, c} is such that the equation

x³ + ax² + bx + c = 0

has three distinct real roots and

(x² + x + 2005)³ + a(x² + x + 2005)² + b(x² + x + 2005) + c > 0

for all real values of x. Show that, for the same set {a, b, c},

(2005)³ + a(2005)² + b(2005) + c > 1/64

Two beggars A and B managed to get a 13-litres-jar full of Vodaka . They have two more jars of 5 and 10 litres respectively. They decided to divide the amount equally, with the aid of the jars and leave the undivided amount for a third beggar C, who was near by. What's the maximum amount the beggars A and B can have, if they are to use only the jars available with them to make the division? Also show the steps to make the division.

Hint: Is it possible to make a division (6 + 6 + 1)?

There are two identical jars W and V, containing equal amounts of Water and Vodka respectively. I take a spoon and transfer a spoonful of Vodka from V to W and dissolve it completely. Now I use the same spoon to transfer a spoonful of the liquid (mixture) from W to V and dissolve it completely.

Now both the jars contain the same amount of liquid, but in diferent ratios of the original components. Which jar has the greater quantity of the other component? That's, whether the Vodka in jar W is more that the Water in the jar V, or the other way?

In a Merry-Go-round, with all seats occupied, the 5th guy is exactly facing the 19th guy. How many seats are there in the Merry-Go-round?

A train leaves station A at x hours y minutes and arrives station B at y hours z minutes. The duration of the journey is z hours x mins. Find all possible value of x, the hour (there could be more than one answers) the train leaves the station A. Assume the clock moves from 00:00 to 24:00.

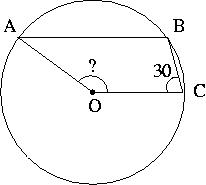
In the above diagram, a line CB is projected from C at an angle 30-degrees from OC., intersecting the circle at B. From B a chord BA parallel to OC is drawn. Find the angle AOC.

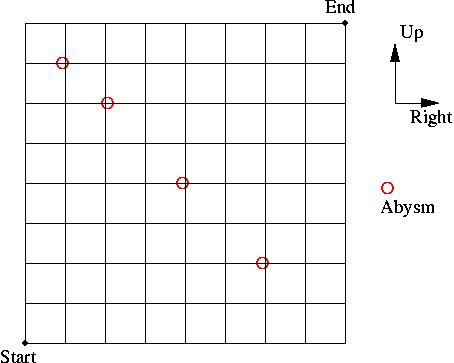
fig1

A drunkard starts from the Start and wants to reach the End. He can move only in the Up and Right directions, along the edges of the small squares, as shown. He can't turn back. On his way there could be abysms, indicated by the circles. He can't reach End if he falls into one of those abysms. What is the probability that the drunkard will reach the End?

fig2

In the above triangle ABC, AB = 3 units and AC = 4 units. The median AD to BC is half of BC in length, as indicated in the figure. Find the area of the triangle ABC.